Cycling learning rate

CLR was proposed by Leslie Smith in 2015. It is an approach to LR adjustments where the value is cycled between a lower bound and upper bound. By nature, it is seen as a competitor to the adaptive LR approaches and hence used mostly with SGD. But it is possible to use it along with the improved optimizers (AdaGrad, AdaDelta, RMSProp, Adam…) with per parameter updates.

CR periodically vary the LR between lower and higher threshold, to remain in a saddle point (a peculiar flat region where the gradient approaches zero when we get to aproximatelly $\alpha=1$. This point is not a local minima, so it is unlikely to get us completely stuck, but it seems like the zzero gradient might slow down learning if we are unluky enough to encounter it. In this situation lower LR can hardly generate enough gradient to come out of it.

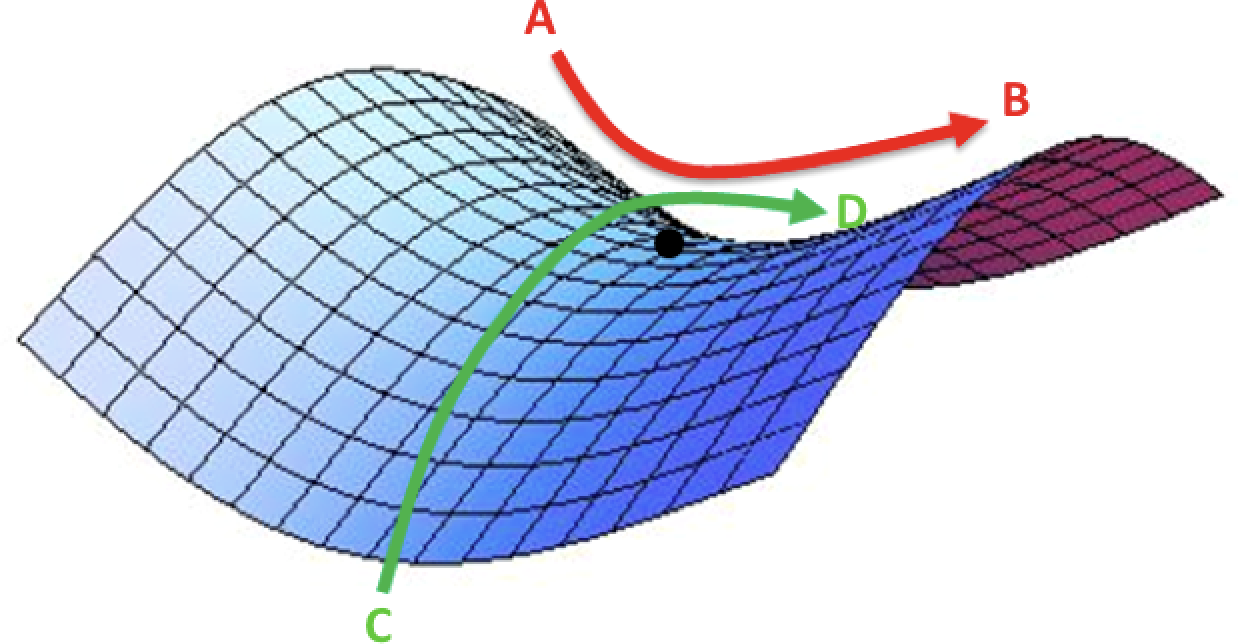
source: safaribooksonline

One solution is to define a variable LR that vary from a $base_lr$ to a $max_lr$ as the ficture:

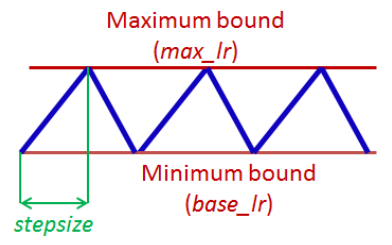
source: Img Credit

def get_triangular_lr(iteration, stepsize, base_lr, max_lr):
    """Given the inputs, calculates the lr that should be applicable for this iteration"""
    cycle = np.floor(1 + iteration/(2  * stepsize))
    x = np.abs(iteration/stepsize - 2 * cycle + 1)
    lr = base_lr + (max_lr - base_lr) * np.maximum(0, (1-x))
    return lr

# Demo of how the LR varies with iterations
num_iterations = 10000
stepsize = 1000
base_lr = 0.0001
max_lr = 0.001
lr_trend = list()

for iteration in range(num_iterations):
    lr = get_triangular_lr(iteration, stepsize, base_lr, max_lr)
    # Update your optimizer to use this learning rate in this iteration
    lr_trend.append(lr)

plt.plot(lr_trend)

The variation optinally can be reduced over time.

Another method proposed by Loshchilov & Hutter [1] in their paper “Sgdr: Stochastic gradient descent with restarts”, called ‘cosine annealing’ in which the learning rate is decreasing from max value following the cosine function and then ‘restarts’ with the maximum at the beginning of the next cycle. Authors also suggest making each next cycle longer than the previous one by some constant factor T_mul.

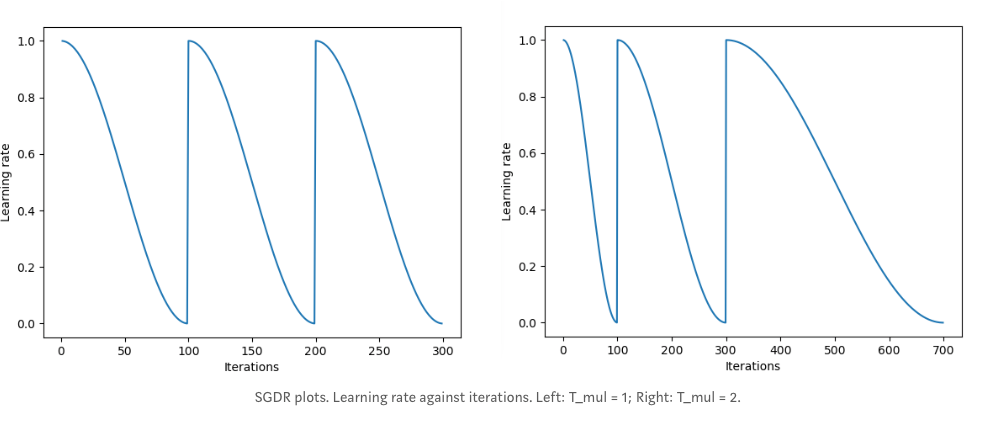
Content source:

The Cyclical Learning Rate technique
Improving the way we work with learning rate

[1] I. Loshchilov and F. Hutter. Sgdr: Stochastic gradient descent with restarts. arXiv preprint arXiv:1608.03983, 2016.