recomendation systems

This post is to resume different options to do make a recomendation system

All recommendations have two components (ther characteristicas could be known or unknown):

items to be recommended, the content (m)
users to recommend items (n)

Content Based recommendation I

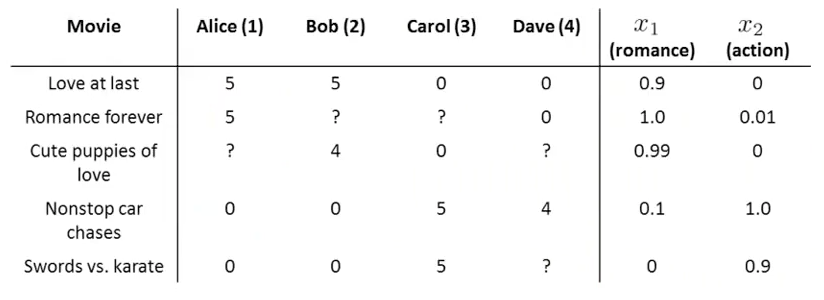
This example is extracted from coursera machine learning course, that basically consists on make a linear regression with the content features and the existing ratings of each user.

It’s important to have some ratings from user on other contents in order to guess his preference from the new content.

$x^{(i)}$ = feature vector for each content ($k$ features).
$\theta^{(j)}$ = parameter vector for user j, $\theta^{(j)} \in \mathbb{R}^{k+1}$ because the bias component

$y^{(i,j)}$ = rating by user j on content i (if defined) $r(i,j) = 1$ if user $j$ has rated the content $i$ (O otherwise)

You have all $x^{(i)}$ bu some $y^{(i,j)}$ are not defined.

Solution: make a linear regresion with known parameters and use the result to compute the gaps: $y^{(i,j)}$

$\underset{\theta^{(j)}}{\text{ argmin }} \dfrac{1}{2m^{(j)}} \sum_{i:r(i,j)=1} ((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2+\dfrac{\lambda}{2m^{(j)}} \sum^n_{k=1} (\theta^{(j)}_k)^2$

Learn $\theta^{(j)}$ (parameter for user j):

$\underset{\theta^{(j)}}{\text{ argmin }} \dfrac{1}{2} \sum_{i:r(i,j)=1} ((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2+\dfrac{\lambda}{2} \sum^n_{k=1} (\theta^{(j)}_k)^2$

Gradient descent update.

Repeat:

$\theta^{(j)}_k = \theta^{(j)}_k - \alpha \sum_{i:r(i,j)=1} ((\theta^{(j)})x^{(i)}-y^{(i,j)})x^{(i)}_k \text{ (for $k=0$)}$ $\theta^{(j)}_k = \theta^{(j)}_k - \alpha \Biggl(\sum_{i:r(i,j)=1} ((\theta^{(j)})x^{(i)}-y^{(i,j)})x^{(i)}_k + \lambda \theta^{(j)}_k\Biggl) \text{ (for $k>0$)}$

For each user $j$, content $i$, compute rating as $(\theta^{(j)})^T(x^{(i)})$

Example colaborative Filtering 1

Colaborative Filtering I

How to retrieve content features from user ratings? The same algorithm but derivative is from $x^{(i)}$:

Learn $x^{(i)}$ (content i):

$\underset{x^{(i)}}{\text{ argmin }} \dfrac{1}{2} \sum_{j:r(i,j)=1} ((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2+\dfrac{\lambda}{2} \sum^n_{k=1} (x^{(i)}_k)^2$

Gradient descent update.

Repeat:

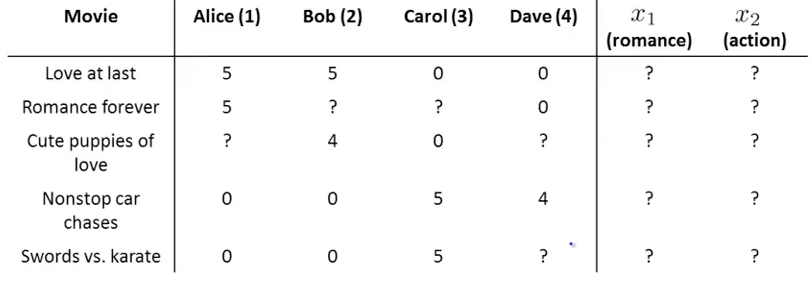
Example colaborative Filtering 2

Colaborative Filtering II

This is the complete colaborative algorithm. Both content features and ratings are calculated from user current ratings $y^{(i,j)}$.

Minimizing $x^{(1)},….x^{(n_m)} \text{ and }\theta^{(1)},….\theta^{(n_u)}$

$\underset{\theta^{(j)} x^{(i)}}{\text{ argmin }} \dfrac{1}{2} \sum_{(i,j):r(i,j)=1} ((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2+\dfrac{\lambda}{2} \sum^{n_m}_{i=1} \sum^n_{k=1} (x^{(i)}_k)^2+\sum^{n_u}_{j=1} \sum^n_{k=1} (\theta^{(j)}_k)^2$

Gradient descent update.

Initialize randomly $x^{(i)}_k$ and $\theta^{(j)}_k$ and repeat:

$x^{(i)}_k = x^{(i)}_k - \alpha \sum_{j:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})\theta^{(j)}_k \text{ (for $k=0$)}$ $x^{(i)}_k = x^{(i)}_k - \alpha \Biggl(\sum_{j:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})\theta^{(j)}_k + \lambda x^{(i)}_k\Biggl) \text{ (for $k>0$)}$ $\theta^{(j)}_k = \theta^{(j)}_k - \alpha \sum_{i:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x^{(i)}_k \text{ (for $k=0$)}$ $\theta^{(j)}_k = \theta^{(j)}_k - \alpha \Biggl(\sum_{i:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x^{(i)}_k + \lambda \theta^{(j)}_k\Biggl) \text{ (for $k>0$)}$