MDPs and Reinforcement Learning

Reinforcement Learning is an area of machine learning. Consists on the best strategies (max reward) that an agent can perform in an environment that is totally or partially known. I’m going to review them in order to focus in Q-Learning that an strong concept behind reinforcement learning.

1. Markov chains

A Markov decission Process (MDP) is a reinterpretation of Markov chains.

Markov chain has the following components:

1. Set of possible $M$ States: $S = \lbrace s_0, s_1,…, s_m \rbrace$
2. Initial State: $s_0$
3. Transition Probabilities Model: $P(s,s’)$

Transition model is a square matrix with the probability transitions from $s$ to $s’$. It has the property that all all rows sum 1:

As an example:

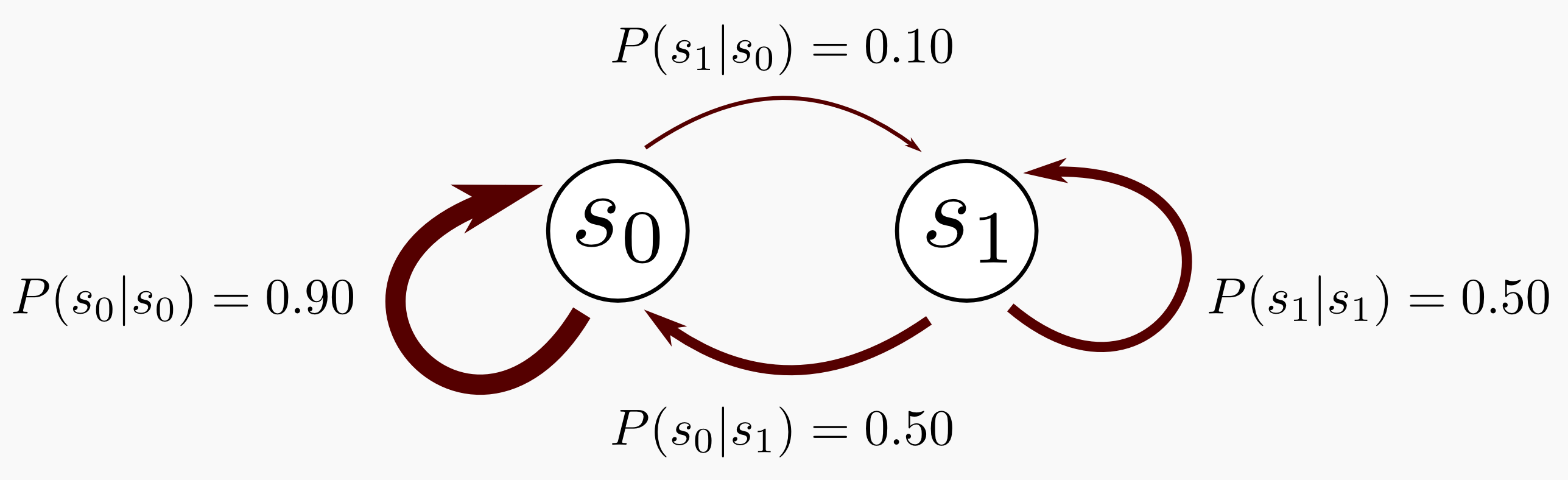
2. Markov decision process (MDP)

A Markov decision process is a extension of a markov chain, including a decision-making agent that observes the environment (described as as set of states $S$) and chooses an action from the given set $A$.

The MDP components:

1. Set of possible $M$ States: $S = \lbrace s_0, s_1,…, s_m \rbrace$
2. Initial State: $s_0$
3. Set of possible $N$ Actions: $A = \lbrace a_0, a_1,…, a_n \rbrace$
4. Transition Probabilities Model: $P(s,a,s’)$ is the probability condition from state $s$ to state $s’$ depending on the action that agent choses.
5. Reward Function: R(s), defined on $S$ which specifies an inmediate reward of being in a given state $s \in S$

Probability conditions from state $s$ to state $s’$ now depend on the action that agent has chosen.

It’s important that Agent knowns (environment is completely observable):

• Transition probability model depending on the action the agent has chosen.
• Reward R(s)

MDP is a stochastic automaton. Decision making is based on maximum expected utility (MEU):

Value Iteration Algorithm (Model based)

This algorithm is from R. Bellman (1957), Bellman demonstrated that value iteration is guaranteed to converge.

inputs:

• $P(s,a,s’)$, a transition-probability matrix
• $R(s)$, a reward matrix
• $\gamma$ typically very near to 1.
• $\epsilon$ typically very near to 0.

returns:

• $U(s)$, the utility matrix

Policy Iteration Algorithm (model based)

If we define the concept of policy, that is the correct strategy for the agent in each state $s$:

Then the same equation can be rewritten as:

No policy generates more reward than the optimal $\pi^{*}$. Policy iteration is guaranteed to converge and at convergence, the current policy and its utility function are the optimal policy and the optimal utility function.

For big State matrix, Policy Iteration Algoritm converges faster than Value Iteration.

inputs:

• $P(s,a,s’)$, a transition-probability matrix
• $\pi(s)$, a policy matrix
• $U(s)$, a utility matrix
• $R(s)$, a reward matrix
• $\gamma$ typically very near to 1.

returns:

• $U(s)$, the utility matrix from policy evaluation

inputs:

• $P(s,a,s’)$, a transition-probability matrix
• $R(s)$, a reward matrix
• $\gamma$ typically very near to 1.

returns:

• $U(s)$, the utility matrix
• $\pi(s)$, the optimal policy

3. Partially Observable Markov decision process (POMDP) - Reinforcement Learning

Until now we have assumed that agent knows S, R, and P, in order to calculate $\pi(s)$ and $U(s)$. This is not often the case in real life applications.

A special class of MDP called Partial observable Markov decision process (POMDP) where rewards and probabilities are not known.

Components:

• $S$ is a set of states
• $A$ is a set of actions
• $T(s’\mid s,a)$ is a set of conditional transition probabilities between states
• $R(s,a)$ a reward function from s and action a
• $\Omega$ a set of observations
• $O(o\mid s’,a)$ a set of conditional observation probabilities
• $\gamma$ [0,1] discount factor.

1. Agent is in some state $s$.
2. Agent takes action $a$.
3. Enviroment transitions to state s’ with probability $T(s’\mid s,a)$. Agesnt does not known the new state.
4. observation $o$ is received with probability $O(o\mid s’,a)$
5. Agent receives a reward R(s,a)

Goal is to maximize its expected future discounted reward: $E [\sum^{\infty}_{t=0} \gamma^tr_t]$

Agent does not know the new state. Insted has a belief of the new state as a probability distribution of the state $b(s)$.

4. Q-Learning (free model)

Model-Free of Reinforcement Learning. Q-learninh finds the optimal action by learning an action-value function called $Q(s,a)$. $Q(s,a)$ represents the maximum discounted future reward when we perform action $a$ in the state $s$, and continue optimally from that point on.

Environment is a black box that receives agent action and returns rewards and new states.

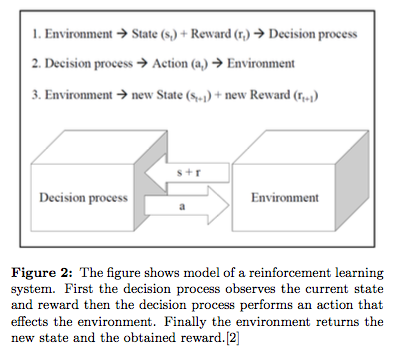
Q-Learning algorithm

Q-Learning retrieves this policy from experience:

Q-Learning algorithm chooses a policy for action selection, related to the action that gives de max Q. All al them have a random value that allows to reach the maximum value.

There is always a compensated relation from Explotation vs Exploitation, explotation gives the best rewards but sometimes is good no to chose the best option in order to explore new ways to reach to a new global maximum or a new maximum that wasn’t before (changing environments). Exploration has a reward cost thats the diference from your expected rewards and expected optimal called Regret.

• $\epsilon$-greedy, always action with max Q is choosen (greediest action), but with probability $\epsilon$ a random action is choosen, thus ensuring optimal actions are discovered.

It you known that world never changes you can lowe $\epsilon$ over time.

• softmax, one drawback of $\epsilon$ is that select random actions uniformly. The worst possible action is likely to be chossen as the second best. In this case a random is selected with regards of the weight associated to each action.

inputs:

• $X$, possible states
• $A$, possible actions
• $\alpha$ [0,1] the learning rate, 0 nothing learned, 0.9 learns quickly
• $\gamma$ [0,1] discount factor. This models that the fact that future rewards are worth less than inmediate reward. Less than 1 to algorithm to converge.

environment (black box):

• $R(s,a)$, reward that environment returns from a state $s$ and action $a$
• $s’$, state that environment returns from a state $s$ and action $a$

returns:

• $U(s)$, the utility matrix
• $\pi(s)$, the optimal policy

SARSA algorithm

The name Sarsa actually comes from the fact that the updates are done using the quintuple $Q(s,a,r,s’,a’)$. The procedural form of Sarsa algorithm is comparable to that of Q-Learning.

Sarsa can overcome Q-Learning in some circunstances searching the optimal path from here.