Clustering k-Means

Introduction to k-Means

k-Means Algorithm allow to partition a set of training data in k clusters in which each observation belongs to the the cluster with the nearest mean. The result is a partition of table called Voronoi cells.

Voronoi cells

Algorithm to find clusters

This algoritm is called Lloyd’s algorithm:

Input:

$K$ (number of clusters)
Training set $\lbrace x^{(1)}, x^{(2)},… x^{(m)} \rbrace; z_i \in \mathbb{R}^n$

Randomy initialize K cluster centroids $\mu_1, \mu_2,…\mu_K \in \mathbb{R}^n$

Repeat {
for $i=1$ to $m$:
$c^{(i)}$ = index ( from 1 to K ) of cluster centroid closest to $x_i$

for $k=1$ to $K$:
$\mu_k$ = average (mean) of points assigned to cluster $k$

} until $c^{(i)}$ are the same as the previous iteration

Proces minimizes with this cost:

$W_k = \sum^K_{k=1} \sum_{x_n \in C_k} ||x_n - \mu_k||^2$

with respect to $C_k$, $\mu_k$

demo

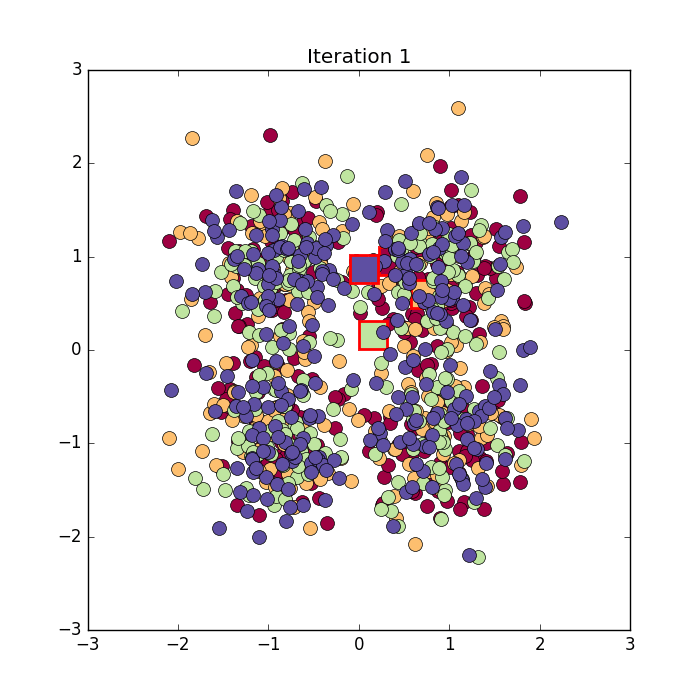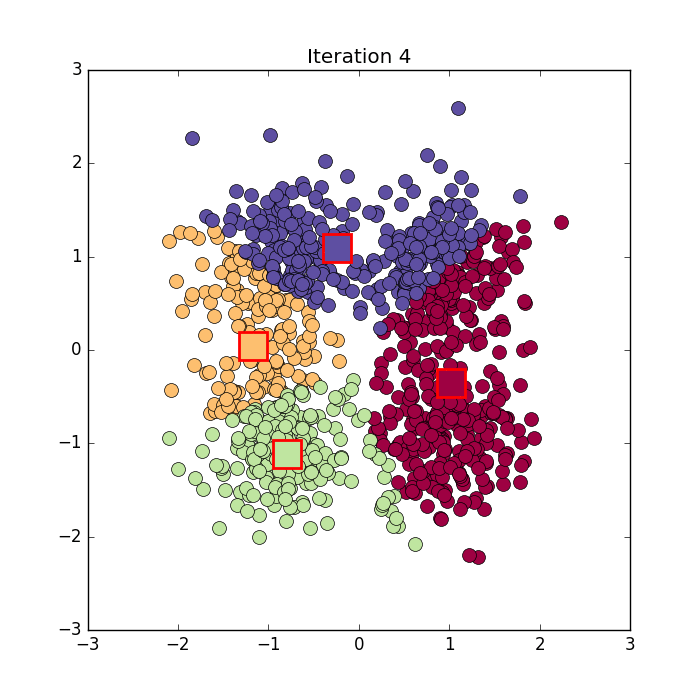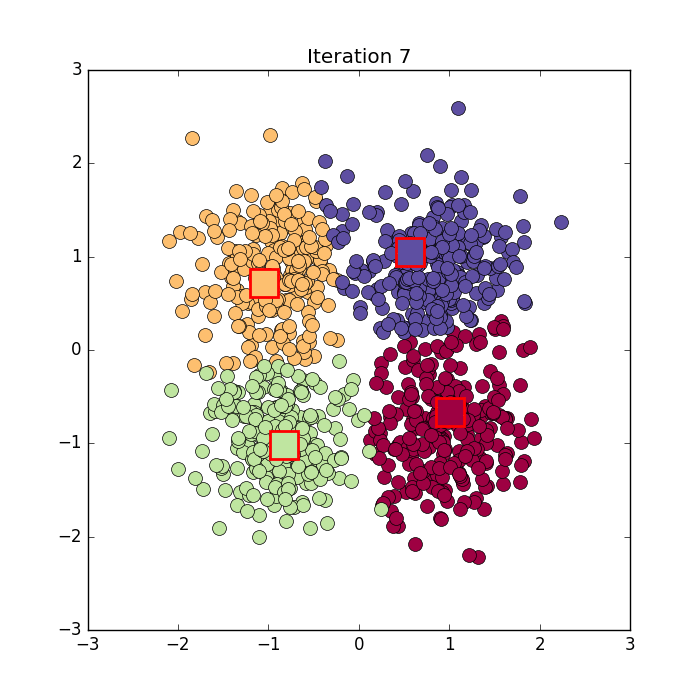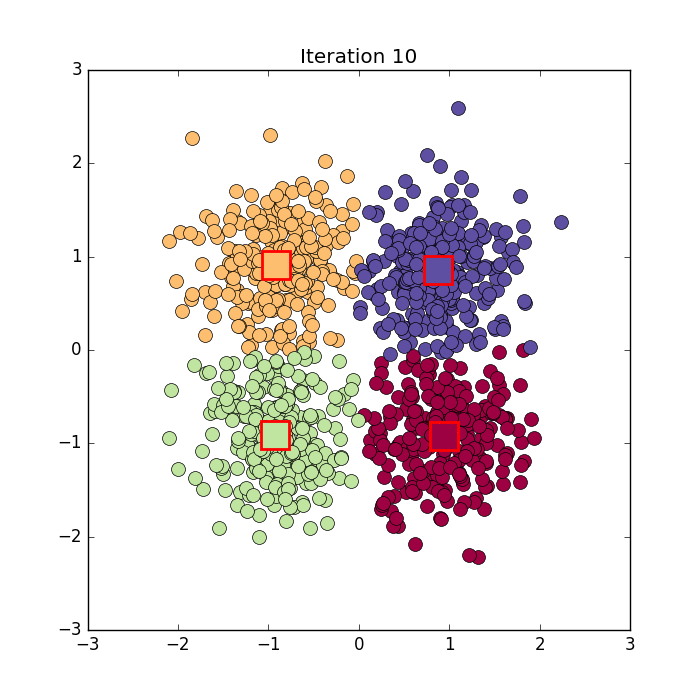
Algorithm in python from here:

import numpy as np
 
def cluster_points(X, mu):
    clusters  = {}
    for x in X:
        bestmukey = min([(i[0], np.linalg.norm(x-mu[i[0]])) \
                    for i in enumerate(mu)], key=lambda t:t[1])[0]
        try:
            clusters[bestmukey].append(x)
        except KeyError:
            clusters[bestmukey] = [x]
    return clusters
 
def reevaluate_centers(mu, clusters):
    newmu = []
    keys = sorted(clusters.keys())
    for k in keys:
        newmu.append(np.mean(clusters[k], axis = 0))
    return newmu
 
def has_converged(mu, oldmu):
    return (set([tuple(a) for a in mu]) == set([tuple(a) for a in oldmu])
 
def find_centers(X, K):
    # Initialize to K random centers
    oldmu = random.sample(X, K)
    mu = random.sample(X, K)
    while not has_converged(mu, oldmu):
        oldmu = mu
        # Assign all points in X to clusters
        clusters = cluster_points(X, mu)
        # Reevaluate centers
        mu = reevaluate_centers(oldmu, clusters)
    return(mu, clusters)

Choosing $K$

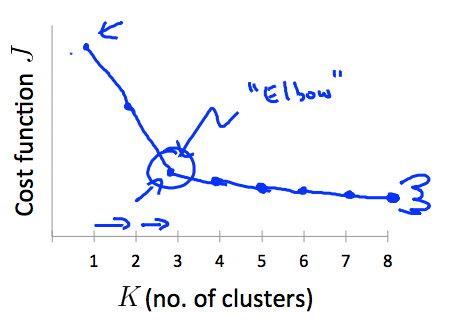
Elbow method:

“elbow” cannot always be unambiguously identified.

elbow

Gap statistic (extracted from here)

It’s a way to standarize to comparison. We evaluate the Gap from a random set of data from the k-Mean for every K.

$Gap_n(k) = \dfrac{1}{B} \sum^B_{b=1} log W^*_{kb} - log W_k$

$W^*_{kb}$ has been generated from a average of $B$ copies generated with Monte Carlo sample distribution.

$\overline w = \dfrac{1}{B} \sum_b log W^*_{kb}$

standar deviation $sd(k)$:

$sd(k) = \sqrt{\dfrac{1}{B} \sum_b (log W^*_{kb}-\overline w)^2)}$ $s_k = \sqrt{1+\dfrac{1}{B}}\cdot sd(k)$

Choose smallest $K$ that satisfies: $Gap(k) \ge Gap(k+1) - s_{k+1}$

We assume that we have computed the k-Mean result from the above algorithm:

def Wk(mu, clusters):
    K = len(mu)
    return sum([np.linalg.norm(mu[i]-c)**2/(2*len(c)) \
               for i in range(K) for c in clusters[i]])

With these cluster results we find the K best aproach.

def find_centers(X, K):
    # Initialize to K random centers
    oldmu = random.sample(X, K)
    mu = random.sample(X, K)
    while not has_converged(mu, oldmu):
        oldmu = mu
        # Assign all points in X to clusters
        clusters = cluster_points(X, mu)
        # Reevaluate centers
        mu = reevaluate_centers(oldmu, clusters)
    return(mu, clusters)



def bounding_box(X):
    xmin, xmax = min(X,key=lambda a:a[0])[0], max(X,key=lambda a:a[0])[0]
    ymin, ymax = min(X,key=lambda a:a[1])[1], max(X,key=lambda a:a[1])[1]
    return (xmin,xmax), (ymin,ymax)
 
def gap_statistic(X):
    (xmin,xmax), (ymin,ymax) = bounding_box(X)
    # Dispersion for real distribution
    ks = range(1,10)
    Wks = zeros(len(ks))
    Wkbs = zeros(len(ks))
    sk = zeros(len(ks))
    for indk, k in enumerate(ks):
        mu, clusters = find_centers(X,k)
        Wks[indk] = np.log(Wk(mu, clusters))
        # Create B reference datasets
        B = 10
        BWkbs = zeros(B)
        for i in range(B):
            Xb = []
            for n in range(len(X)):
                Xb.append([random.uniform(xmin,xmax),
                          random.uniform(ymin,ymax)])
            Xb = np.array(Xb)
            mu, clusters = find_centers(Xb,k)
            BWkbs[i] = np.log(Wk(mu, clusters))
        Wkbs[indk] = sum(BWkbs)/B
        sk[indk] = np.sqrt(sum((BWkbs-Wkbs[indk])**2)/B)
    sk = sk*np.sqrt(1+1/B)
    return(ks, Wks, Wkbs, sk)