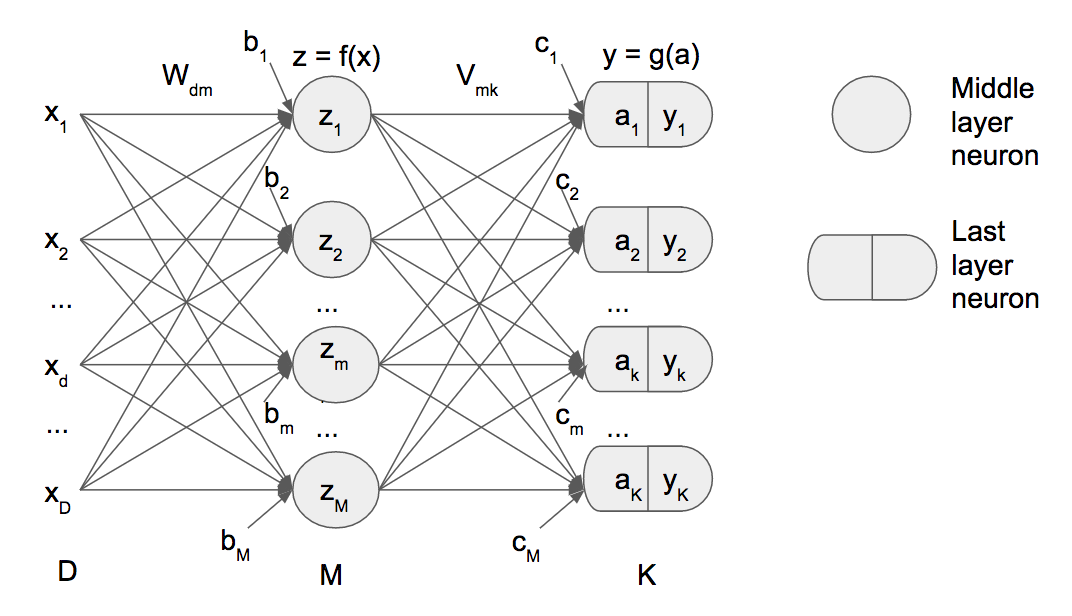
Neural network L1 and L2 regulatization

Demonstration of L1 and L2 regularization in back recursive propagation on neural networks

Purpose of this post is to show that additional calculations in case of regularization L1 or L2.

Regularization ins a technique to prevent neural networks (and logistics also) to over-fit. Over-fitting occurs when you train a neural network that predicts fully your trained data but predicts poorly on any new test data.

Regularization increases error (or reduces likelihood).

The two most common forms of regularization are called L1 and L2. In L2 regularization (the most common of the two forms), you modify the error function you use during training to include an additional term that adds a fraction (usually given Greek letter lower case lambda) of the sum of the squared values of the weights. So larger weight values lead to larger error, and therefore the training algorithm favors and generates small weight values.

basic network example

L1 regression consists of search min of cross entropy error:

$Min (\sum_{n=1}^N \sum_{k=1}^K t_k^{(n)}ln(y_k^{(n)}))$

as well as satisfy the constraint that

$\sum_k \beta^2 <= s$

From lagrange multiplier we can write the above equation as,

$Min \Biggl(\sum_{n=1}^N \sum_{k=1}^K t_k^{(n)}ln(y_k^{(n)}) + \lambda\sum_k (\beta^2 - s)\Biggl)$

$s$ is a constant so we can write the above equation as:

$Min \Biggl(\sum_{n=1}^N \sum_{k=1}^K t_k^{(n)}ln(y_k^{(n)}) + \lambda\sum_k \beta^2\Biggl)$

L2 regularization is also known as Ridge Regression.

$Ln(P(Y=T|X))=\underbrace{\sum_{n=1}^N \sum_{k=1}^K t_k^{(n)}ln(y_k^{(n)})}_{\text{cross entropy error}}+\underbrace{\dfrac{\lambda}{2n}\sum_m\sum_kV^2_{mk}+\dfrac{\lambda}{2n}\sum_d\sum_mW^2_{dm}}_{\text{penalty term}}$ $V_{mk} = V_{mk} + \dfrac{\alpha}{n} \sum_n ( t^{(n)}_k-y^{(n)}_k)z^{(n)}_m + \dfrac{\lambda}{n}V_{mk}$ $W_{dm} = W_{dm}-\dfrac{\alpha}{n} \sum_n \sum_{k} ( t^{(n)}_k - y^{(n)}_k) V_{mk}z^{(n)}_m(1-z^{(n)}_m)x^{(n)}_d + \dfrac{\lambda}{n}W_{dm}$

L1 regularization is also known as LASSO.

$Ln(P(Y=T|X))=\underbrace{\sum_{n=1}^N \sum_{k=1}^K t_k^{(n)}ln(y_k^{(n)})}_{\text{cross entropy error}}+\underbrace{\dfrac{\lambda}{n}\sum_m\sum_k|V_{mk}|+\dfrac{\lambda}{n}\sum_d\sum_m|W_{dm}|}_{\text{penalty term}}$ $V_{mk} = V_{mk} + \dfrac{\alpha}{n} \sum_n ( t^{(n)}_k-y^{(n)}_k)z^{(n)}_m + \dfrac{\lambda}{n}sign(V_{mk})$ $W_{dm} = W_{dm}+\dfrac{\alpha}{n} \sum_n \sum_{k} ( t^{(n)}_k + y^{(n)}_k) V_{mk}z^{(n)}_m(1-z^{(n)}_m)x^{(n)}_d + \dfrac{\lambda}{n}sign(W_{dm})$

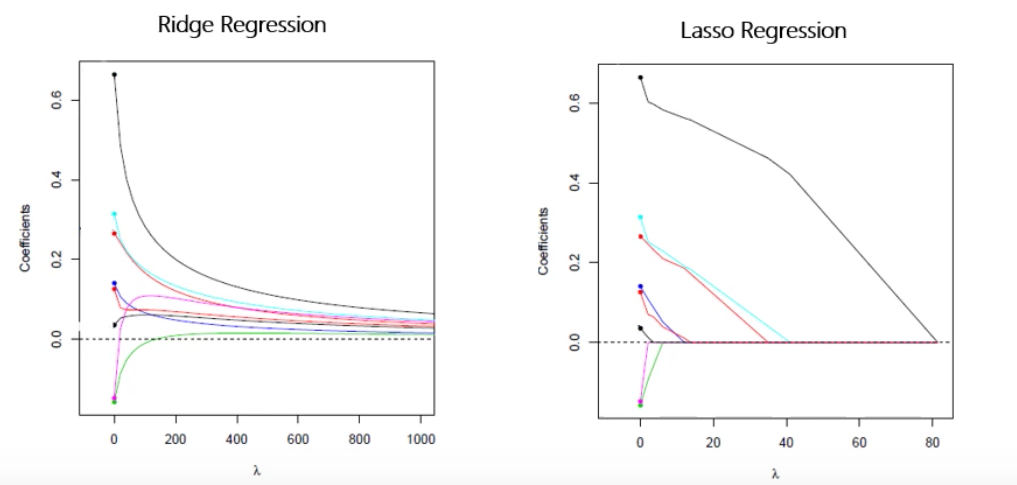
The turning parameter $\lambda$ in both cases controls the weight of the penalty. Increase $\lambda$ in LASSO causes least significance coefs to be shrunken to 0, and is a way to select the best features.

LASSO

source: Data Science - Part XII - Ridge Regression, LASSO, and Elastic Nets

Intuition:

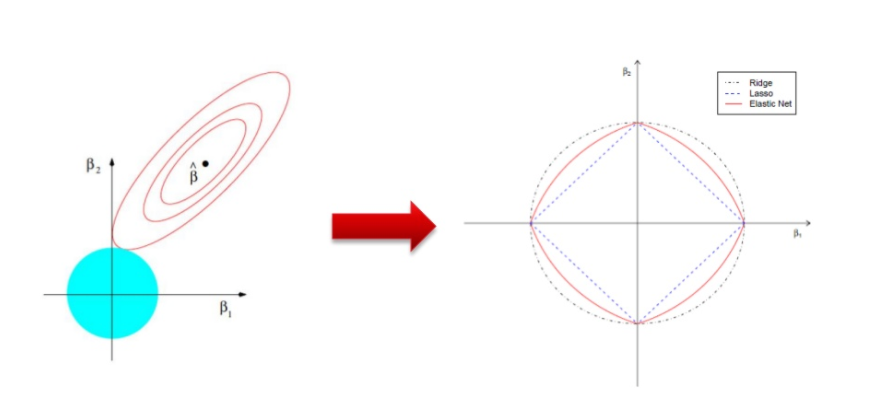
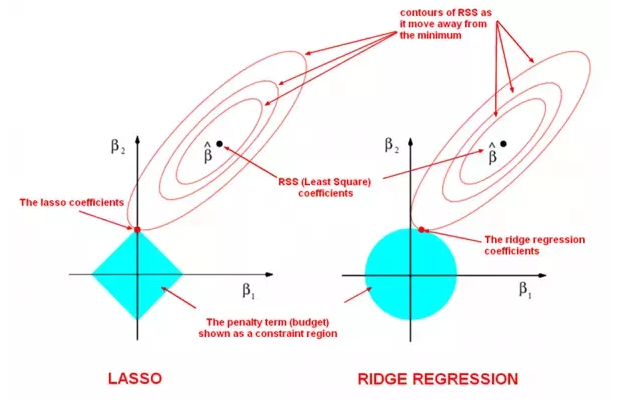
If $f(\beta)$ is the objective function like the cross entropy error, The minimum is in the middle of the circles, that is the non penalized solucion.

If we add a different objective $g(\beta)$ with colour blue in the graph, we get that larger $\lambda$ gets a “narrow” contour plot.

Now we have to find the minimum of the sum of this two objectives: $f(\beta)+g(\beta)$. And this is achieved when two contour plots meet each other.

LASSO will probably meet in a corner that makes some $\beta$ to be 0 and this is useful to feature selection. This does not happen in the Ridge regression.

regularization coefs

source: source of graph

A general form for penalty term can be writen as:

$P_\alpha = \sum^K_{k=1} ( \dfrac{1}{2}(1-\alpha)\beta^2_k + \alpha|\beta|)$ $P_\alpha = \begin{cases} \text{Ridge regression} & \text{if $\alpha$ = 0} \\ \text{LASSO} & \text{if $\alpha$ = 1} \\ \text{elastic net} & \text{if 0 < $\alpha$ < 1 } \end{cases}$

elastic net